Trong thế giới toán học, các con số tự nhiên được xây dựng từ những thành phần cơ bản. Giống như một bức tường được xây nên từ những viên gạch, những thành phần đó chính là thừa số. Đây là một trong những khái niệm đầu tiên và quan trọng nhất mà chúng ta được học trong số học. Vậy thực chất thừa số là gì và tại sao việc hiểu về nó lại quan trọng đến vậy? Việc nắm vững khái niệm thừa số, đặc biệt là thừa số nguyên tố, là chìa khóa. Nó giúp mở ra cánh cửa để giải quyết vô số các bài toán phức tạp hơn sau này. Bài viết này sẽ cung cấp một cái nhìn toàn diện, giúp bạn hiểu rõ bản chất thừa số là gì.
Giải Thích Chi Tiết: Thừa Số Là Gì?
Để có một cái nhìn đúng đắn, chúng ta cần tìm hiểu về định nghĩa và phân biệt nó với các khái niệm liên quan.
1. Định Nghĩa Về Thừa Số Trong Phép Nhân
Thừa số là gì? Trong một phép tính nhân, thừa số (tiếng Anh: Factor) là bất kỳ số nào được nhân với một số khác để tạo ra một kết quả. Kết quả của phép nhân đó được gọi là tích số (product). Nói một cách đơn giản, các số hạng tham gia vào phép nhân đều được gọi là thừa số.
Ví dụ cơ bản:
- Trong phép nhân 3 x 5 = 15.
- Số 3 và số 5 được gọi là các thừa số.
- Số 15 được gọi là tích số.
Một khái niệm liên quan chặt chẽ là “ước số” (divisor). Nếu một số a là thừa số của số c, thì a cũng là ước số của c. Điều này có nghĩa là c chia hết cho a. Trong ví dụ trên, 3 và 5 là các thừa số của 15, đồng thời chúng cũng là các ước số của 15.
2. Mối Quan Hệ Giữa Thừa Số và Tích Số
Mối quan hệ giữa thừa số và tích số là mối quan hệ nền tảng của phép nhân.
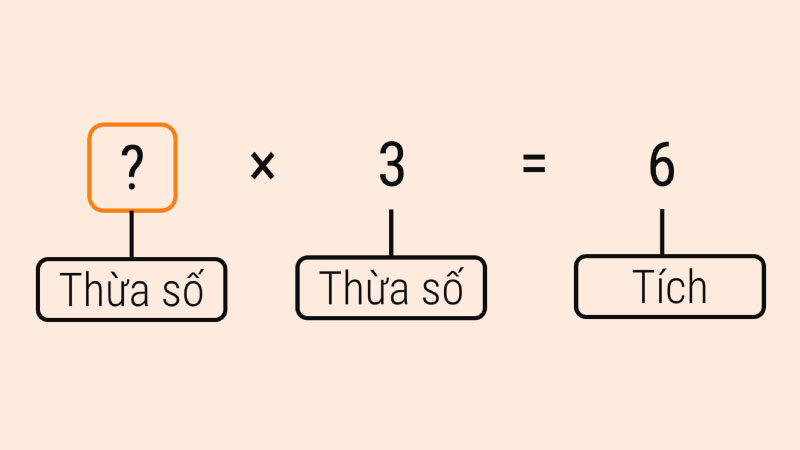
- Thừa số × Thừa số = Tích số
Từ mối quan hệ này, chúng ta có thể suy ra các quy tắc quan trọng trong toán học tiểu học.
- Tìm một thừa số chưa biết: Muốn tìm một thừa số, ta lấy tích số chia cho thừa số đã biết.
- Tính chất giao hoán: Thay đổi vị trí của các thừa số không làm thay đổi tích số (a x b = b x a).
- Tính chất kết hợp: Khi nhân một tích hai số với số thứ ba, ta có thể nhân số thứ nhất. Với tích của số thứ hai và số thứ ba ((a x b) x c = a x (b x c)).
Hiểu rõ mối quan hệ này là bước đầu tiên để trả lời câu hỏi thừa số là gì.
3. Phân Biệt Cốt Lõi: Thừa Số (Factor) và Số Hạng (Term)
Đây là một điểm rất quan trọng thường gây nhầm lẫn cho học sinh.
Thừa số (Factor):
- Là các thành phần trong một phép nhân.
- Ví dụ: Trong 7 x 2 = 14, 7 và 2 là các thừa số.
Số hạng (Term):
- Là các thành phần trong một phép cộng.
- Ví dụ: Trong 7 + 2 = 9, 7 và 2 là các số hạng.
Việc sử dụng sai thuật ngữ giữa thừa số và số hạng có thể dẫn đến những hiểu lầm. Và sai sót nghiêm trọng khi giải các bài toán phức tạp hơn. Luôn nhớ rằng, “thừa số” đi liền với phép nhân, còn “số hạng” đi liền với phép cộng.
Thừa Số Nguyên Tố: Khái Niệm Nền Tảng Của Số Học
Khái niệm về thừa số trở nên đặc biệt quan trọng khi chúng ta nói về số nguyên tố.
1. Ôn Lại Về Số Nguyên Tố và Hợp Số
Số nguyên tố (Prime Number):

- Là số tự nhiên lớn hơn 1, chỉ có đúng hai ước số là 1 và chính nó.
- Ví dụ: 2, 3, 5, 7, 11, 13…
- Số 2 là số nguyên tố chẵn duy nhất.
Hợp số (Composite Number):
- Là số tự nhiên lớn hơn 1, có nhiều hơn hai ước số.
- Ví dụ: 4 (có các ước 1, 2, 4), 6 (có các ước 1, 2, 3, 6), 9 (có các ước 1, 3, 9)…
- Mọi hợp số đều có thể được phân tích thành tích của các số nguyên tố.
Việc phân biệt hai loại số này là nền tảng để hiểu về thừa số nguyên tố.
2. Thừa Số Nguyên Tố Là Gì?
Thừa số nguyên tố của một số tự nhiên là các ước số của số đó và đồng thời là số nguyên tố. Nói cách khác, khi chúng ta phân tích một số thành tích của các số khác nhau. Những thừa số nào trong phép nhân đó là số nguyên tố thì chúng được gọi là thừa số nguyên tố.
Ví dụ:
- Số 12 có các ước số là: 1, 2, 3, 4, 6, 12.
- Trong các ước số này, 2 và 3 là các số nguyên tố. Do đó, 2 và 3 là các thừa số nguyên tố của 12.
- Chúng ta có thể viết 12 thành tích của các thừa số nguyên tố: 12 = 2 x 2 x 3 = 2² x 3.
Việc tìm ra các thừa số nguyên tố của một số được gọi là “phân tích một số ra thừa số nguyên tố”. Đây là một trong những kỹ năng quan trọng nhất trong số học. Việc tìm hiểu thừa số là gì sẽ không hoàn chỉnh nếu thiếu khái niệm này.
3. Định Lý Cơ Bản Của Số Học
Tầm quan trọng của thừa số nguyên tố được khẳng định bởi Định lý Cơ bản của Số học. Định lý này phát biểu rằng: “Mọi số nguyên lớn hơn 1 hoặc là một số nguyên tố, hoặc có thể được biểu diễn dưới dạng tích của các thừa số nguyên tố, và sự biểu diễn này là duy nhất nếu không kể đến thứ tự của các thừa số”.
Điều này có nghĩa là mỗi một hợp số đều có một “dấu vân tay” hay một “mã DNA” duy nhất. Được tạo thành từ các thừa số nguyên tố của nó, một tính chất rất đặc biệt. Ví dụ, số 12 sẽ luôn luôn được phân tích thành hai số 2 và một số 3 (2² x 3). Không có một tổ hợp thừa số nguyên tố nào khác có thể nhân lại với nhau để ra 12. Định lý này là nền tảng cho rất nhiều lĩnh vực trong toán học và khoa học máy tính. Bao gồm cả lĩnh vực mật mã học, một ứng dụng cực kỳ quan trọng.
Hướng Dẫn Cách Phân Tích Một Số Ra Thừa Số Nguyên Tố
Có hai phương pháp phổ biến để phân tích một số ra thừa số nguyên tố.
1. Phương pháp Chia Lần Lượt (Trial Division)
Đây là phương pháp phổ biến và có hệ thống nhất, thường được dạy trong trường học.
- Bước 1: Lấy số cần phân tích (gọi là N) chia cho số nguyên tố nhỏ nhất là 2.
- Bước 2: Nếu N chia hết cho 2, ta viết N dưới dạng 2 x (N/2). Lấy kết quả thương (N/2) và tiếp tục lặp lại Bước 1.
- Bước 3: Nếu N không chia hết cho 2, ta tiếp tục chia nó cho số nguyên tố tiếp theo là 3.
- Bước 4: Lặp lại quá trình này, chia cho các số nguyên tố theo thứ tự tăng dần (2, 3, 5, 7, 11…). Cho đến khi thương cuối cùng là 1, ta dừng lại.
- Bước 5: Viết N dưới dạng tích của tất cả các số nguyên tố đã dùng để chia.
Cách trình bày phổ biến là kẻ một đường thẳng đứng, số cần phân tích ở bên trái. Và các thừa số nguyên tố ở bên phải, đây là một cách rất trực quan.
2. Phương pháp Sơ Đồ Cây (Factor Tree)
Đây là một phương pháp trực quan hơn, đặc biệt hữu ích với các số không quá lớn.
- Bước 1: Viết số cần phân tích (N) ở trên cùng.
- Bước 2: Tìm hai thừa số bất kỳ có tích bằng N và viết chúng ở dưới, nối với N bằng hai nhánh cây.
- Bước 3: Nếu một trong hai thừa số đó là số nguyên tố, hãy khoanh tròn nó lại.
- Bước 4: Nếu một thừa số là hợp số, tiếp tục phân tích nó thành hai thừa số nhỏ hơn.
- Bước 5: Lặp lại quá trình cho đến khi tất cả các nhánh cuối cùng đều là các số nguyên tố đã được khoanh tròn.
- Bước 6: Tích của tất cả các số nguyên tố đã được khoanh tròn chính là dạng phân tích.
3. Ví dụ Phân tích chi tiết số 36 và 100 ra thừa số nguyên tố
Phân tích số 36:
- Cách 1 (Chia lần lượt):
- 36 | 2
- 18 | 2
- 9 | 3
- 3 | 3
- 1
- Kết quả: 36 = 2 x 2 x 3 x 3 = 2² x 3².
- Cách 2 (Sơ đồ cây):
- 36 -> 4 x 9
- 4 -> 2 x 2
- 9 -> 3 x 3
- Kết quả: 36 = 2 x 2 x 3 x 3 = 2² x 3².
Phân tích số 100:
- Cách 1 (Chia lần lượt):
- 100 | 2
- 50 | 2
- 25 | 5
- 5 | 5
- 1
- Kết quả: 100 = 2 x 2 x 5 x 5 = 2² x 5².
Ứng Dụng Của Việc Phân Tích Thừa Số Nguyên Tố
Việc phân tích ra thừa số nguyên tố có rất nhiều ứng dụng quan trọng.
1. Tìm Ước Chung Lớn Nhất (ƯCLN – GCD)
Để tìm ƯCLN của hai hay nhiều số, ta thực hiện các bước sau:
- Phân tích mỗi số ra thừa số nguyên tố.
- Chọn ra các thừa số nguyên tố chung.
- Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
- Ví dụ: Tìm ƯCLN(36, 100).
- 36 = 2² x 3²
- 100 = 2² x 5²
- Thừa số nguyên tố chung là 2, với số mũ nhỏ nhất là 2.
- Vậy, ƯCLN(36, 100) = 2² = 4.
2. Tìm Bội Chung Nhỏ Nhất (BCNN – LCM)
Để tìm BCNN của hai hay nhiều số, ta thực hiện các bước sau:
- Phân tích mỗi số ra thừa số nguyên tố.
- Chọn ra các thừa số nguyên tố chung và riêng.
- Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.
- Ví dụ: Tìm BCNN(36, 100).
- 36 = 2² x 3²
- 100 = 2² x 5²
- Các thừa số nguyên tố chung và riêng là 2, 3, 5. Số mũ lớn nhất tương ứng là 2, 2, 2.
- Vậy, BCNN(36, 100) = 2² x 3² x 5² = 4 x 9 x 25 = 900.
3. Ứng Dụng Trong Mật Mã Học (Cryptography)
Đây là một trong những ứng dụng hiện đại và quan trọng nhất của thừa số nguyên tố. Hệ thống mã hóa khóa công khai RSA, một trong những nền tảng của an ninh mạng. (Bảo mật cho website, email, giao dịch ngân hàng…), hoạt động dựa trên một nguyên tắc. Nguyên tắc đó là: việc nhân hai số nguyên tố rất lớn với nhau thì rất dễ dàng. Nhưng việc phân tích một số khổng lồ thành hai thừa số nguyên tố của nó lại cực kỳ khó khăn về mặt tính toán. Khóa công khai chính là con số khổng lồ đó, trong khi khóa bí mật chứa hai thừa số nguyên tố gốc. Sự khó khăn của việc phân tích thừa số chính là bức tường bảo mật cho dữ liệu.
Kết Luận
Qua những phân tích chi tiết trên, hy vọng bạn đã có một câu trả lời toàn diện cho câu hỏi “thừa số là gì?”. Đây là một khái niệm toán học cơ bản nhưng lại là viên gạch nền tảng cho toàn bộ ngành số học. Từ những phép nhân đơn giản đến việc phân tích một số ra thừa số nguyên tố. Hay các ứng dụng phức tạp như tìm ƯCLN, BCNN và cả trong lĩnh vực mật mã học hiện đại. Khái niệm thừa số luôn đóng một vai trò trung tâm và không thể thiếu được.
Việc nắm vững định nghĩa, phân biệt được thừa số với số hạng và thành thạo các phương pháp. Các phương pháp phân tích một số ra thừa số nguyên tố là một kỹ năng cực kỳ quan trọng. Nó không chỉ giúp các em học sinh học tốt môn toán mà còn rèn luyện tư duy logic. Cùng với đó là khả năng phân tích và giải quyết vấn đề một cách có hệ thống. Hiểu rõ thừa số là gì chính là bước đầu tiên trên hành trình khám phá vẻ đẹp. Và sức mạnh của những con số, nền tảng của mọi ngành khoa học.