Home » Khối lập phương là gì? Tính chất và công thức tính thể tích

Khối lập phương là gì? Tính chất và công thức tính thể tích

12 lượt xem

Trong thế giới hình học không gian, khối lập phương là một trong những hình khối cơ bản và quen thuộc nhất. Từ những viên xúc xắc, những khối rubik đến những viên đường nhỏ, hình ảnh của nó xuất hiện ở khắp mọi nơi. Mặc dù quen thuộc, không phải ai cũng nắm vững tất cả các tính chất và công thức liên quan. Vậy thực chất khối lập phương là gì và nó có những đặc điểm toán học nào đáng chú ý? Việc hiểu rõ bản chất, tính chất và các công thức của khối lập phương là kiến thức nền tảng. Nó không chỉ quan trọng trong chương trình học mà còn có nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện, giúp bạn trả lời câu hỏi khối lập phương là gì.

Giải Thích Chi Tiết: Khối Lập Phương Là Gì?

Để có một cái nhìn khoa học, chúng ta cần tìm hiểu về định nghĩa và vị trí của nó trong toán học.

1. Định Nghĩa Hình Học Về Khối Lập Phương

Khối lập phương là gì? Trong hình học Euclid, khối lập phương (tiếng Anh: Cube) là một khối đa diện đều ba chiều. Nó được giới hạn bởi sáu mặt hình vuông bằng nhau. Mỗi đỉnh của khối lập phương là nơi giao nhau của ba cạnh. Và các cạnh gặp nhau tại mỗi đỉnh đều tạo thành một góc vuông. Do tất cả các mặt đều là hình vuông và bằng nhau, tất cả các cạnh có độ dài bằng nhau. Và tất cả các góc trong đều là góc vuông, nên khối lập phương được xem là một hình khối hoàn hảo. Nó có mức độ đối xứng rất cao trong không gian ba chiều.

Khối lập phương còn có tên gọi khác là hình hexahedron đều (regular hexahedron), trong đó “hexa” có nghĩa là sáu. Và “hedron” có nghĩa là mặt, tức là một khối có sáu mặt đều. Nó là một trường hợp đặc biệt của hình hộp chữ nhật mà tất cả các cạnh đều có độ dài bằng nhau. Sự đơn giản, cân đối và hoàn hảo trong cấu trúc đã khiến khối lập phương. Trở thành một trong những đối tượng được nghiên cứu nhiều nhất và sớm nhất trong lịch sử toán học.

2. Mối Quan Hệ Giữa Hình Vuông và Hình Lập Phương

Để dễ hình dung, chúng ta có thể xem khối lập phương là phiên bản ba chiều (3D) của hình vuông hai chiều (2D). Nếu hình vuông là một hình phẳng được giới hạn bởi bốn cạnh bằng nhau và bốn góc vuông. Thì khối lập phương là một hình khối được giới hạn bởi sáu mặt hình vuông bằng nhau. Quá trình “nâng cấp” từ hình vuông lên hình lập phương có thể được tưởng tượng. Bằng cách lấy một hình vuông và “kéo” nó ra theo một chiều không gian thứ ba. Với một khoảng cách bằng đúng độ dài cạnh của hình vuông ban đầu.

Mối quan hệ này còn được thể hiện qua các công thức tính toán. Diện tích của một hình vuông là $a^{2}$ (cạnh nhân cạnh). Và thể tích của một khối lập phương là $a^{3}$ (cạnh nhân cạnh nhân cạnh). Sự tương đồng này giúp chúng ta dễ dàng ghi nhớ và suy luận các tính chất. Từ không gian hai chiều quen thuộc sang không gian ba chiều một cách logic và trực quan. Đây là một khái niệm quan trọng khi tìm hiểu khối lập phương là gì.

3. Khối Lập Phương Trong Nhóm 5 Khối Đa Diện Đều Platon

Khối lập phương có một vị trí rất đặc biệt trong lịch sử hình học. Nó là một trong năm khối đa diện đều Platon duy nhất tồn tại. Đây là các khối đa diện lồi mà tất cả các mặt đều là các đa giác đều bằng nhau. Và tại mỗi đỉnh có cùng một số mặt gặp nhau, tạo nên sự đối xứng hoàn hảo. Năm khối đa diện đều Platon bao gồm:

Khối tứ diện đều (Tetrahedron): 4 mặt là tam giác đều.
Khối lập phương (Hexahedron/Cube): 6 mặt là hình vuông.
Khối bát diện đều (Octahedron): 8 mặt là tam giác đều.
Khối mười hai mặt đều (Dodecahedron): 12 mặt là ngũ giác đều.
Khối hai mươi mặt đều (Icosahedron): 20 mặt là tam giác đều.

Các khối đa diện này đã được nhà triết học Hy Lạp Platon nghiên cứu và mô tả. Ông gán cho mỗi khối một nguyên tố cổ điển (Lửa, Đất, Khí, Nước) và Vũ trụ. Trong đó, khối lập phương được gán cho nguyên tố Đất, tượng trưng cho sự ổn định và vững chắc.

Các Yếu Tố và Tính Chất Cơ Bản Của Khối Lập Phương

Một khối lập phương được cấu thành từ các yếu tố cơ bản và có những tính chất hình học đặc trưng.

1. Các Yếu Tố Cấu Thành: Đỉnh, Cạnh và Mặt

Một khối lập phương luôn có một số lượng đỉnh, cạnh và mặt cố định.

6 Mặt (Faces): Khối lập phương có tổng cộng 6 mặt. Tất cả các mặt này đều là những hình vuông hoàn toàn bằng nhau về diện tích. Các mặt đối diện của khối lập phương luôn song song với nhau.
12 Cạnh (Edges): Khối lập phương có tổng cộng 12 cạnh. Tất cả 12 cạnh này đều có độ dài bằng nhau. Mỗi cạnh là đoạn thẳng nối hai đỉnh liền kề với nhau.
8 Đỉnh (Vertices): Khối lập phương có tổng cộng 8 đỉnh. Mỗi đỉnh là giao điểm của ba mặt và ba cạnh của khối lập phương.

Mối quan hệ giữa số đỉnh (V), số cạnh (E) và số mặt (F) của khối lập phương. Nó tuân theo công thức Euler cho đa diện lồi: $V - E + F = 2$ (tức là $8 - 12 + 6 = 2$ ).

2. Các Tính Chất Về Sự Đối Xứng và Bằng nhau

Do được cấu tạo từ các hình vuông bằng nhau, khối lập phương có rất nhiều tính chất đối xứng.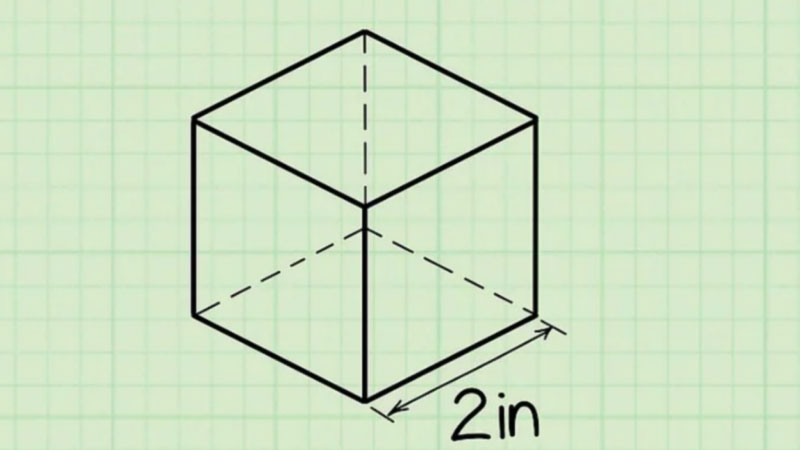

Tất cả các cạnh đều bằng nhau: Nếu gọi độ dài một cạnh là $a$ , thì tất cả 12 cạnh đều có độ dài là $a$ .
Tất cả các mặt đều là hình vuông bằng nhau: Mỗi mặt đều có diện tích là $a^{2}$ .
Tất cả các góc ở các đỉnh đều là góc vuông: Các cạnh gặp nhau tại mỗi đỉnh đều vuông góc với nhau.
Tính đối xứng cao: Khối lập phương có nhiều mặt phẳng đối xứng và trục đối xứng. Nó có thể được quay hoặc phản chiếu theo nhiều cách mà vẫn giữ nguyên hình dạng.

Chính những tính chất này làm cho khối lập phương trở thành một hình khối rất đặc biệt. Và thường được sử dụng làm mô hình cơ bản trong nhiều lĩnh vực khoa học, nghệ thuật.

3. Đường Chéo của Mặt và Đường Chéo của Khối

Trong một khối lập phương, chúng ta cần phân biệt hai loại đường chéo khác nhau.

Đường chéo của mặt (Face Diagonal): Đây là đoạn thẳng nối hai đỉnh đối diện của cùng một mặt hình vuông.

Mỗi mặt hình vuông có hai đường chéo, do đó khối lập phương có tổng cộng $6 \times 2 = 12$ đường chéo mặt. . Tất cả 12 đường chéo mặt này đều có độ dài bằng nhau.

Đường chéo của khối (Space Diagonal): Đây là đoạn thẳng nối hai đỉnh đối diện của toàn bộ khối lập phương. Hai đỉnh này không cùng nằm trên một mặt. Khối lập phương có tổng cộng 4 đường chéo khối. Tất cả 4 đường chéo khối này đều có độ dài bằng nhau và chúng cắt nhau tại tâm của khối lập phương.

Việc phân biệt hai loại đường chéo này rất quan trọng khi tính toán các công thức liên quan.

Các Công Thức Tính Toán Quan Trọng Của Khối Lập Phương

Gọi $a$ là độ dài cạnh của khối lập phương, chúng ta có các công thức sau.

1. Công Thức Tính Diện Tích Xung Quanh

Diện tích xung quanh của một khối lập phương là tổng diện tích của bốn mặt bên. Do mỗi mặt là một hình vuông có diện tích là $a^{2}$ , nên diện tích xung quanh sẽ là:

S_{x q} = 4 \times a^{2}

Ví dụ: Một khối lập phương có cạnh dài 5 cm. Diện tích xung quanh của nó là: $S_{x q} = 4 \times (5 c m)^{2} = 4 \times 25 c m^{2} = 100 c m^{2}$ .

Công thức này rất hữu ích khi bạn cần tính toán lượng vật liệu cần thiết. Để che phủ bốn mặt bên của một vật thể hình lập phương, chẳng hạn như giấy dán tường.

2. Công Thức Tính Diện Tích Toàn Phần

Diện tích toàn phần của một khối lập phương là tổng diện tích của tất cả sáu mặt. Vì khối lập phương có 6 mặt hình vuông bằng nhau, công thức tính rất đơn giản:

S_{tp} = 6 \times a^{2}

Ví dụ: Vẫn với khối lập phương có cạnh dài 5 cm. Diện tích toàn phần của nó là: $S_{tp} = 6 \times (5 c m)^{2} = 6 \times 25 c m^{2} = 150 c m^{2}$ .

Công thức này rất quan trọng khi bạn cần tính lượng vật liệu để làm một chiếc hộp hình lập phương. Hoặc lượng sơn cần thiết để sơn tất cả các mặt của một khối lập phương.

3. Công Thức Tính Thể Tích Khối Lập Phương

Thể tích của một khối lập phương là lượng không gian mà khối đó chiếm giữ. Nó được tính bằng cách nhân chiều dài, chiều rộng và chiều cao lại với nhau. Do cả ba kích thước này đều bằng $a$ , nên công thức tính thể tích là:

V = a \times a \times a = a^{3}

Ví dụ: Khối lập phương có cạnh dài 5 cm sẽ có thể tích là: Thể tích của nó là: $V = (5 c m)^{3} = 125 c m^{3}$ .

Đây là một trong những công thức cơ bản và quan trọng nhất khi tìm hiểu khối lập phương là gì. Nó được ứng dụng rộng rãi để tính toán dung tích của các vật thể.

4. Công Thức Tính Độ Dài Đường Chéo

Đường chéo của mặt ( $d_{f}$ ): . Áp dụng định lý Pytago cho tam giác vuông tạo bởi hai cạnh và đường chéo của một mặt. Ta có: $d_{f 2} = a^{2} + a^{2} = 2 a^{2}$ . . Do đó, độ dài đường chéo của một mặt là:

d_{f} = a 2

Đường chéo của khối ( $d_{s}$ ): . Áp dụng định lý Pytago cho tam giác vuông tạo bởi một cạnh, đường chéo của mặt đáy. Và đường chéo của khối. Ta có: $d_{s 2} = a^{2} + d_{f 2}$ . Do đó, độ dài đường chéo của khối là:

d_{s} = a 3

Kết Luận

Qua những phân tích chi tiết trên, hy vọng bạn đã có một câu trả lời toàn diện cho câu hỏi “khối lập phương là gì?”. Đây là một hình khối 3D cơ bản nhưng lại chứa đựng sự hoàn hảo về mặt toán học. Với 6 mặt vuông bằng nhau, 12 cạnh bằng nhau và 8 đỉnh, nó là biểu tượng của sự cân đối. Việc nắm vững các tính chất và các công thức tính diện tích, thể tích của khối lập phương. Nó không chỉ là kiến thức nền tảng trong chương trình học mà còn có rất nhiều ứng dụng.

Từ kiến trúc, thiết kế đến các vật dụng quen thuộc trong đời sống hàng ngày. Hình ảnh của khối lập phương luôn hiện diện, cho thấy tầm quan trọng của nó. Hãy thực hành vẽ hình, áp dụng các công thức vào các bài tập cụ thể. Để có thể làm chủ hoàn toàn kiến thức về hình khối đặc biệt này. Việc hiểu sâu về những khái niệm cơ bản sẽ là nền tảng vững chắc để bạn chinh phục. Bạn có thể chinh phục những kiến thức hình học không gian phức tạp hơn trong tương lai.