Home » Hằng đẳng thức là gì? Các công thức và mẹo ghi nhớ nhanh

Hằng đẳng thức là gì? Các công thức và mẹo ghi nhớ nhanh

3 lượt xem

27/10/2025
9:55 sáng
Blog

Trong hành trình khám phá thế giới toán học, đặc biệt là lĩnh vực đại số, có những công cụ giống như những chiếc chìa khóa vạn năng. Chúng giúp chúng ta mở ra những cánh cửa phức tạp, biến những biểu thức rắc rối trở nên đơn giản hơn rất nhiều. Một trong những bộ chìa khóa quan trọng nhất mà mọi học sinh cần phải nắm vững chính là các hằng đẳng thức. Chúng xuất hiện xuyên suốt chương trình toán học phổ thông. Chúng là nền tảng cho rất nhiều dạng bài tập khác nhau. Vậy thực sự hằng đẳng thức là gì? Chúng có những công thức nào và làm thế nào để ghi nhớ chúng một cách hiệu quả nhất? Bài viết này sẽ là một cẩm nang toàn diện.

Hằng đẳng thức là gì? Khái niệm nền tảng trong Đại số

Trước khi học thuộc lòng các công thức, việc hiểu rõ bản chất và vai trò của hằng đẳng thức là bước đầu tiên và quan trọng nhất. Nó giúp việc học trở nên ý nghĩa hơn.

Định nghĩa cơ bản: Khi đẳng thức luôn luôn đúng

Hãy bắt đầu với định nghĩa đơn giản nhất. Hằng đẳng thức là gì? Đó là một đẳng thức (một phương trình có dấu bằng) mà luôn luôn đúng với mọi giá trị của các biến số có mặt trong đẳng thức đó. Từ “hằng” ở đây có nghĩa là “luôn luôn”, “bất biến”. Điều này khác hoàn toàn với một phương trình thông thường. Một phương trình như $x + 2 = 5$ chỉ đúng khi $x = 3$ . Nhưng một hằng đẳng thức như $(A + B)^2 = A^2 + 2AB + B^2$ thì lại luôn đúng. Dù bạn thay A và B bằng bất kỳ số nào hay biểu thức nào, dấu bằng vẫn sẽ xảy ra.

Hãy thử kiểm tra. Nếu $A=1, B=2$ , vế trái là $(1+2)^2 = 3^2 = 9$ . Vế phải là $1^2 + 2(1)(2) + 2^2 = 1 + 4 + 4 = 9$ . Hai vế bằng nhau. Nếu $A=x, B=y$ , vế trái là $(x+y)^2$ . Vế phải là $x^2 + 2xy + y^2$ . Chúng ta biết rằng $(x+y)^2$ chính là $(x+y)(x+y) = x^2 + xy + yx + y^2 = x^2 + 2xy + y^2$ . Hai vế vẫn luôn bằng nhau. Tính chất “luôn đúng” này chính là bản chất cốt lõi của hằng đẳng thức.

Tại sao cần học hằng đẳng thức? “Vũ khí bí mật” của người học toán

Việc ghi nhớ và vận dụng thành thạo các hằng đẳng thức mang lại vô số lợi ích cho người học toán. Chúng không chỉ là những công thức khô khan. Chúng là những công cụ tư duy mạnh mẽ.

Rút gọn biểu thức: Các biểu thức đại số phức tạp thường có thể được đơn giản hóa một cách nhanh chóng nếu bạn nhận ra dạng của một hằng đẳng thức.
Tính toán nhanh: Bạn có thể tính nhẩm giá trị của các biểu thức số học một cách ấn tượng. Ví dụ như tính $101^2$ hay $49 \times 51$ .
Phân tích đa thức thành nhân tử: Đây là một trong những ứng dụng quan trọng nhất. Các hằng đẳng thức như hiệu hai bình phương hay tổng/hiệu hai lập phương là chìa khóa để phân tích đa thức. Kỹ năng này lại là nền tảng để giải phương trình và bất phương trình bậc cao.
Nền tảng cho kiến thức cao hơn: Các hằng đẳng thức là kiến thức cơ bản. Chúng sẽ tiếp tục được sử dụng trong các phần toán phức tạp hơn ở các cấp học cao hơn. Ví dụ như trong lượng giác, giải tích hay đại số tuyến tính.Vì vậy, việc đầu tư thời gian để làm chủ các công thức này là một sự đầu tư hoàn toàn xứng đáng.

7 Hằng đẳng thức đáng nhớ và các công thức mở rộng

Trong chương trình toán học phổ thông, có 7 hằng đẳng thức cơ bản mà mọi học sinh đều cần phải thuộc lòng. Chúng ta sẽ đi qua từng công thức một cách chi tiết.

1. (A + B)² – Bình phương của một tổng: Nền tảng đầu tiên

Đây là hằng đẳng thức đầu tiên và cơ bản nhất. Nó mô tả cách khai triển bình phương của một biểu thức có hai số hạng cộng lại.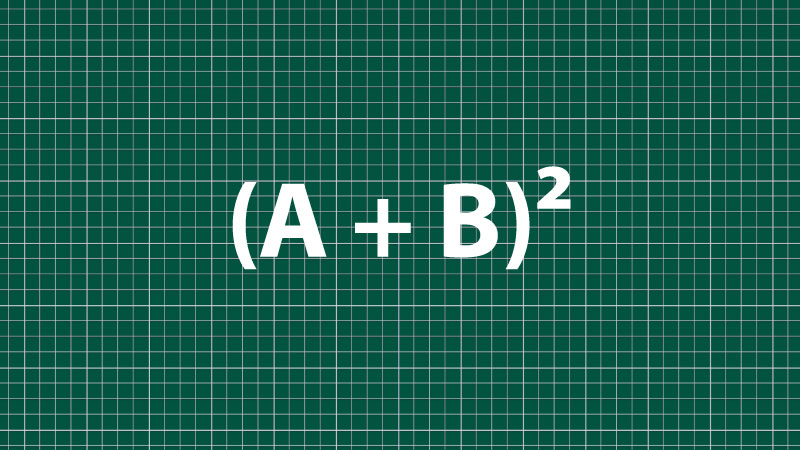

Công thức:

(A + B)^2 = A^2 + 2AB + B^2

Diễn giải: Bình phương của một tổng bằng bình phương số hạng thứ nhất. Cộng với hai lần tích của số hạng thứ nhất và số hạng thứ hai. Cộng với bình phương số hạng thứ hai.

Ví dụ 1 (Số học): Tính 51²

Ta viết 51 = 50 + 1. Áp dụng công thức, ta có:

(50 + 1)² = 50² + 2 x 50x 1 + 1² = 2500 + 100 + 1 = 2601.

Ví dụ 2 (Đại số): Khai triển (x + 3y)².

Áp dụng công thức với A=x và B=3y, ta có:

(x + 3y)² = x² + 2(x)(3y) + (3y)² = x² + 6xy + 9y².

Mẹo ghi nhớ: Hãy nhớ quy tắc “bình phương số đầu, hai lần tích hai số, bình phương số cuối”. Dấu ở giữa luôn là dấu cộng.

2. (A – B)² – Bình phương của một hiệu: Sự thay đổi nhỏ về dấu

Hằng đẳng thức này rất giống với công thức đầu tiên. Điểm khác biệt duy nhất nằm ở dấu của số hạng ở giữa.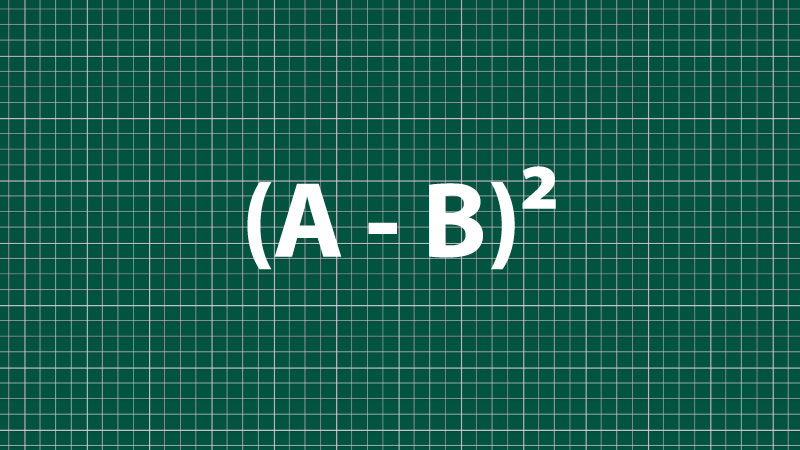

Công thức:

(A - B)^2 = A^2 - 2AB + B^2

Diễn giải: Bình phương của một hiệu bằng bình phương số hạng thứ nhất. Trừ đi hai lần tích của số hạng thứ nhất và số hạng thứ hai. Cộng với bình phương số hạng thứ hai.

Ví dụ 1 (Số học): Tính 49².

Ta viết 49 = 50 – 1. Áp dụng công thức, ta có:

(50 – 1)² = 50² – 2x50x 1 + 1² = 2500 – 100 + 1 = 2401.

Ví dụ 2 (Đại số): Khai triển (2x – 5)².

Áp dụng công thức với A=2x và B=5, ta có:

(2x – 5)² = (2x)² – 2(2x)(5) + 5² = 4x² – 20x + 25.

Mẹo ghi nhớ: Quy tắc giống hệt bình phương của tổng. Chỉ cần nhớ đổi dấu cộng ở giữa thành dấu trừ. Dấu cuối cùng vẫn là dấu cộng.

3. A² – B² – Hiệu hai bình phương: Công cụ phân tích nhân tử mạnh mẽ

Đây là một trong những hằng đẳng thức được ứng dụng nhiều nhất. Nó giúp biến đổi một hiệu thành một tích.

Công thức:

A² - B² = (A - B)(A + B)

Diễn giải: Hiệu của hai bình phương bằng tích của hiệu hai số đó và tổng hai số đó.

Ví dụ 1 (Số học): Tính nhanh 51 \times 49.

Ta nhận thấy 51 = 50 + 1 và 49 = 50 – 1. Áp dụng công thức theo chiều ngược lại, ta có:

51x 49 = (50 + 1)(50 – 1) = 50² – 1² = 2500 – 1 = 2499.

Ví dụ 2 (Đại số): Phân tích đa thức 9x² – 4y² thành nhân tử.

Ta nhận thấy 9x² = (3x)² và 4y² = (2y)². Áp dụng công thức với A=3x và B=2y, ta có:

9x² – 4y² = (3x)² – (2y)² = (3x – 2y)(3x + 2y).

Mẹo ghi nhớ: Hãy nhớ tên gọi “hiệu hai bình phương”. Kết quả luôn là một tích của (“hiệu” nhân “tổng”).

4. (A + B)³ – Lập phương của một tổng: Bước lên bậc ba

Hằng đẳng thức này mô tả cách khai triển lập phương của một tổng.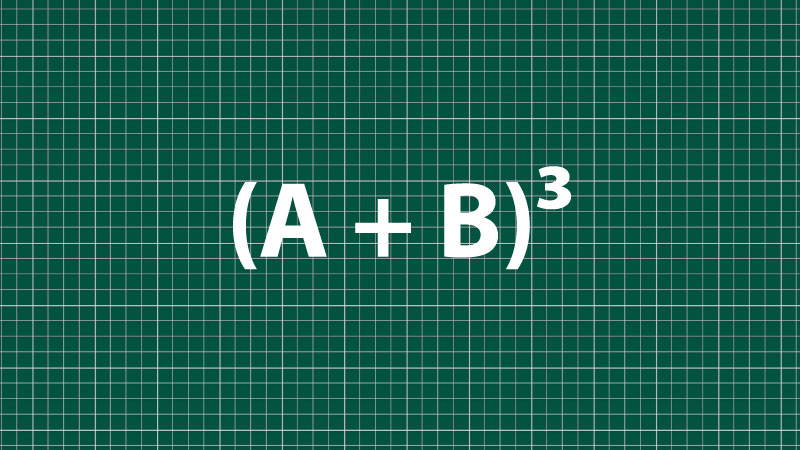

Công thức:

(A + B)^3 = A^3 + 3A^2B + 3AB^2 + B^3

Diễn giải: Lập phương của một tổng bằng lập phương số hạng thứ nhất. Cộng ba lần tích bình phương số thứ nhất với số thứ hai. Cộng ba lần tích số thứ nhất với bình phương số thứ hai. Cộng lập phương số hạng thứ hai.

Ví dụ: Khai triển (x + 2)³

Áp dụng công thức với A=x và B=2, ta có:

(x + 2)³ = x^3 + 3(x²)(2) + 3(x)(2²) + 2³ = x³ + 6x² + 12x + 8

Mẹo ghi nhớ: Các hệ số là 1, 3, 3, 1 (giống hàng thứ 4 của tam giác Pascal). Số mũ của A giảm dần từ 3 về 0. Số mũ của B tăng dần từ 0 lên 3. Tất cả các dấu đều là dấu cộng.

5. (A – B)³ – Lập phương của một hiệu: Quy tắc dấu xen kẽ

Tương tự như bình phương, hằng đẳng thức lập phương của một hiệu rất giống với lập phương của tổng. Chỉ có sự thay đổi về dấu.

Công thức:

(A - B)^3 = A^3 - 3A^2B + 3AB^2 - B^3

Diễn giải: Tương tự như lập phương của tổng, nhưng các dấu sẽ xen kẽ: +, -, +, -.

Ví dụ: Khai triển (y – 3)³

Áp dụng công thức với A=y và B=3, ta có:

(y – 3)³ = y³ – 3(y²)(3) + 3(y)(3²) – 3³ = y³ – 9y^2 + 27y – 27

Mẹo ghi nhớ: Các hệ số và số mũ giống hệt lập phương của tổng (1, 3, 3, 1). Chỉ cần nhớ quy tắc dấu xen kẽ: cộng, trừ, cộng, trừ.

6. A³ + B³ – Tổng hai lập phương: Phân tích thành tích (Phần 1)

Hằng đẳng thức này và công thức tiếp theo là công cụ quan trọng để phân tích đa thức thành nhân tử.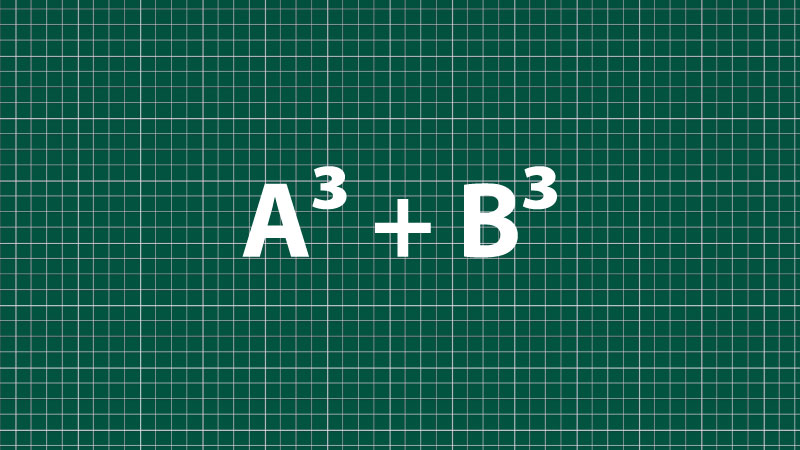

Công thức:

A^3 + B^3 = (A + B)(A^2 - AB + B^2)

Diễn giải: Tổng của hai lập phương bằng tích của tổng hai số đó với “bình phương thiếu của hiệu”. (Biểu thức A² – AB + B² được gọi là bình phương thiếu vì nó giống (A-B)^2 nhưng chỉ có một lần AB).

Ví dụ: Phân tích x³ + 8 thành nhân tử.

Ta nhận thấy 8 = 2³. Áp dụng công thức với A=x và B=2, ta có:

x³ + 8 = x³ + 2³ = (x + 2)(x² – x (2) + 2²) = (x + 2)(x² – 2x + 4).

Mẹo ghi nhớ: Nhân tử đầu tiên có dấu giống hệt biểu thức gốc (A + B). Dấu của số hạng AB trong nhân tử thứ hai luôn ngược lại. Dấu cuối cùng luôn là dấu cộng.

7. A³ – B³ – Hiệu hai lập phương: Phân tích thành tích (Phần 2)

Đây là hằng đẳng thức cuối cùng trong bộ 7 công thức cơ bản.

Công thức:

A³ - B³ = (A - B)(A^2 + AB + B^2)

Diễn giải: Hiệu của hai lập phương bằng tích của hiệu hai số đó với “bình phương thiếu của tổng”.

Ví dụ: Phân tích 27y³ – 1 thành nhân tử.

Ta nhận thấy 27y³ = (3y)³ và 1 = 1³. Áp dụng công thức với A=3y và B=1, ta có:

27y³ – 1 = (3y³ – 1³ = (3y – 1)((3y)² + (3y)(1) + 1²) = (3y – 1)(9y² + 3y + 1)

Mẹo ghi nhớ: Quy tắc dấu giống như tổng hai lập phương. Nhân tử đầu tiên (A – B) có dấu giống biểu thức gốc. Dấu của AB trong nhân tử thứ hai ngược lại. Dấu cuối cùng luôn là cộng.

Mẹo ghi nhớ nhanh và cách tránh những sai lầm “chết người”

Việc nhớ chính xác các công thức là rất quan trọng. Dưới đây là một vài chiến lược giúp bạn học thuộc và tránh các lỗi sai phổ biến.

Chiến lược học thuộc lòng khoa học và hiệu quả

Hiểu bản chất trước khi thuộc: Đừng chỉ học vẹt. Hãy tự mình khai triển các biểu thức $(A+B)^2$ , $(A-B)^2$ , $(A+B)(A-B)$ … để hiểu tại sao công thức lại như vậy.
Sử dụng Flashcards: Viết tên hằng đẳng thức ở mặt trước và công thức ở mặt sau. Thường xuyên tự kiểm tra.
Viết đi viết lại: Chép lại các công thức nhiều lần vào một cuốn sổ tay riêng.
Liên kết các công thức: Nhóm các công thức có cấu trúc tương tự lại với nhau (ví dụ: nhóm bình phương, nhóm lập phương khai triển, nhóm lập phương phân tích). So sánh sự giống và khác nhau giữa chúng.
Dạy lại cho người khác: Hãy thử giải thích các công thức này cho một người bạn. Việc giảng dạy lại là cách tốt nhất để củng cố kiến thức.Việc áp dụng các phương pháp này sẽ giúp bạn ghi nhớ hằng đẳng thức lâu hơn.

Các lỗi sai kinh điển và cách khắc phục triệt để

Ngay cả những học sinh khá giỏi đôi khi cũng mắc phải những lỗi sai rất cơ bản khi áp dụng hằng đẳng thức.

Lỗi sai số 1: $(A + B)^2 = A^2 + B^2$ ??? Đây là lỗi sai phổ biến nhất. Rất nhiều bạn quên mất số hạng $2AB$ ở giữa. Cách khắc phục: Luôn nhớ rằng bình phương của một tổng/hiệu có BA số hạng.
Lỗi sai số 2: $(A - B)^2 = A^2 - B^2$ ??? Tương tự như trên, các bạn quên số hạng $-2AB$ và nhầm lẫn với công thức hiệu hai bình phương. Cách khắc phục: Nhớ rõ tên gọi: “Bình phương của một hiệu” khác với “Hiệu hai bình phương”.
Lỗi sai về dấu trong công thức lập phương: Các công thức lập phương có nhiều dấu cộng trừ hơn, dễ gây nhầm lẫn. Đặc biệt là dấu của số hạng $AB$ trong công thức tổng/hiệu hai lập phương. Cách khắc phục: Học thuộc quy tắc dấu xen kẽ (+, -, +, -) cho $(A-B)^3$ . Học thuộc quy tắc “dấu đầu giống, dấu giữa ngược, dấu cuối luôn cộng” cho $A^3 \pm B^3$
Lỗi sai khi A hoặc B là biểu thức phức tạp: Khi áp dụng công thức cho $(2x + 3y)^2$ , nhiều bạn chỉ bình phương $x$ và $y$ mà quên bình phương cả hệ số. Ví dụ viết thành $2x^2$ thay vì $(2x)^2 = 4x^2$ . Cách khắc phục: Luôn sử dụng dấu ngoặc đơn cẩn thận khi thay A và B bằng các biểu thức.

Kết luận

Các hằng đẳng thức không chỉ là những công thức toán học khô khan. Chúng là những quy luật đẹp đẽ và có tính hệ thống của đại số. Chúng là những công cụ mạnh mẽ giúp chúng ta đơn giản hóa vấn đề, tăng tốc độ tính toán và giải quyết các bài toán phức tạp một cách hiệu quả. Việc dành thời gian để hiểu rõ, ghi nhớ chính xác và luyện tập thường xuyên với 7 hằng đẳng thức đáng nhớ này là một sự đầu tư vô cùng quan trọng. Nó sẽ là nền tảng vững chắc cho bạn trên con đường chinh phục những đỉnh cao mới của toán học.