Trong chương trình hình học, đặc biệt là từ lớp 6, các em học sinh bắt đầu làm quen. Với nhiều khái niệm nền tảng quan trọng, trong đó có tia phân giác của một góc. Đây là một khái niệm cơ bản nhưng lại có rất nhiều tính chất và ứng dụng thú vị. Nó xuất hiện trong nhiều bài toán từ đơn giản đến phức tạp về sau này. Vậy thực chất tia phân giác là gì và làm thế nào để xác định nó một cách chính xác? Bài viết này sẽ cung cấp một cái nhìn toàn diện, giúp các em học sinh và phụ huynh. Hiểu rõ bản chất tia phân giác là gì, cách vẽ và các tính chất quan trọng liên quan.
Các Khái Niệm Cơ Bản Cần Nắm Vững Trước Khi Tìm Hiểu Tia Phân Giác
Để hiểu sâu về tia phân giác, trước tiên chúng ta cần ôn lại một vài khái niệm hình học cơ bản. Đây là những viên gạch nền tảng không thể thiếu trong quá trình học tập của các em.
1. Tia (Ray) Trong Hình Học Là Gì?
Trong hình học Euclid, một tia là một phần của một đường thẳng. Nó có một điểm bắt đầu cố định, gọi là gốc, và kéo dài vô tận về một phía. Hãy tưởng tượng một tia sáng phát ra từ một chiếc đèn pin, đó chính là hình ảnh trực quan nhất. Ánh sáng bắt đầu từ bóng đèn (gốc) và chiếu thẳng, kéo dài mãi mãi về một hướng. Khi vẽ một tia trên giấy, chúng ta thường vẽ một điểm làm gốc. Sau đó kẻ một đường thẳng từ điểm đó và có thể thêm một mũi tên ở đầu kia. Để biểu thị rằng nó kéo dài vô tận và không có điểm kết thúc ở phía đó.
Một tia thường được đặt tên bằng hai chữ cái in hoa. Chữ cái đầu tiên luôn là tên của điểm gốc, và chữ cái thứ hai là một điểm bất kỳ. Một điểm bất kỳ khác nằm trên tia đó để xác định hướng của nó. Ví dụ, tia Ox là tia có gốc tại điểm O và đi qua điểm x. Hiểu rõ khái niệm tia là rất quan trọng vì tia phân giác cũng chính là một tia. Nó có những đặc điểm và tính chất hình học rất đặc biệt mà chúng ta sẽ tìm hiểu.
2. Góc (Angle) Được Tạo Thành Như Thế Nào?
Góc là một hình hình học được tạo bởi hai tia có chung một điểm gốc. Điểm gốc chung này được gọi là đỉnh của góc, và hai tia đó được gọi là hai cạnh của góc. Góc thể hiện “độ mở” hay khoảng không gian giữa hai cạnh này. Trong cuộc sống hàng ngày, chúng ta gặp hình ảnh của góc ở khắp mọi nơi. Ví dụ như góc tạo bởi hai kim đồng hồ, góc của một mái nhà, góc mở của một cánh cửa.
Một góc thường được đặt tên bằng ba chữ cái in hoa, với chữ cái ở giữa là tên của đỉnh. Ví dụ, góc xOy là góc có đỉnh tại O, hai cạnh là hai tia Ox và Oy. Đôi khi, người ta cũng có thể gọi tên góc bằng tên của đỉnh (ví dụ: góc O). Hoặc đặt một số hay một chữ cái Hy Lạp nhỏ bên trong để ký hiệu. Hiểu được cấu tạo của một góc là điều kiện tiên quyết để có thể hiểu được khái niệm. Khái niệm về việc chia một góc thành hai phần bằng nhau, tức là tia phân giác.
3. Cách Đo và Đọc Số Đo Của Một Góc
Độ lớn của một góc được đo bằng một đơn vị gọi là độ (°). Dụng cụ phổ biến nhất để đo góc trong chương trình học là thước đo góc (hay thước đo độ). Thước đo góc thường có hình nửa hình tròn, được chia thành 180 vạch bằng nhau, mỗi vạch ứng với 1 độ. Để đo một góc, bạn đặt tâm của thước trùng với đỉnh của góc. Sau đó, điều chỉnh một cạnh của góc đi qua vạch số 0 trên thước đo. Cạnh còn lại của góc chỉ vào vạch nào trên thước, đó chính là số đo của góc đó.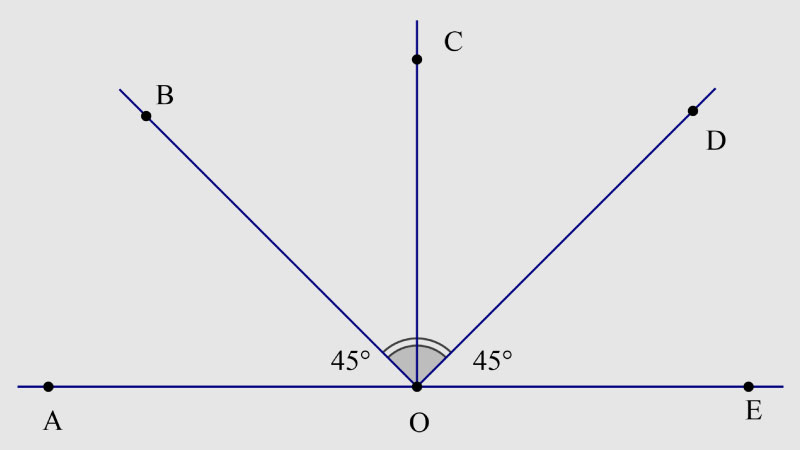
Dựa trên số đo, các góc được phân loại thành:
- Góc nhọn: Có số đo lớn hơn 0° và nhỏ hơn 90°.
- Góc vuông: Có số đo bằng đúng 90°.
- Góc tù: Có số đo lớn hơn 90° và nhỏ hơn 180°.
- Góc bẹt: Có số đo bằng đúng 180°, hai cạnh của nó tạo thành một đường thẳng.
Việc đo góc chính xác là kỹ năng cần thiết để có thể vẽ được tia phân giác bằng thước đo độ.
Giải Thích Chi Tiết: Tia Phân Giác Là Gì?
Bây giờ, chúng ta sẽ đi vào định nghĩa và các tính chất cốt lõi của tia phân giác.
1. Định Nghĩa Chính Xác Về Tia Phân Giác Của Một Góc
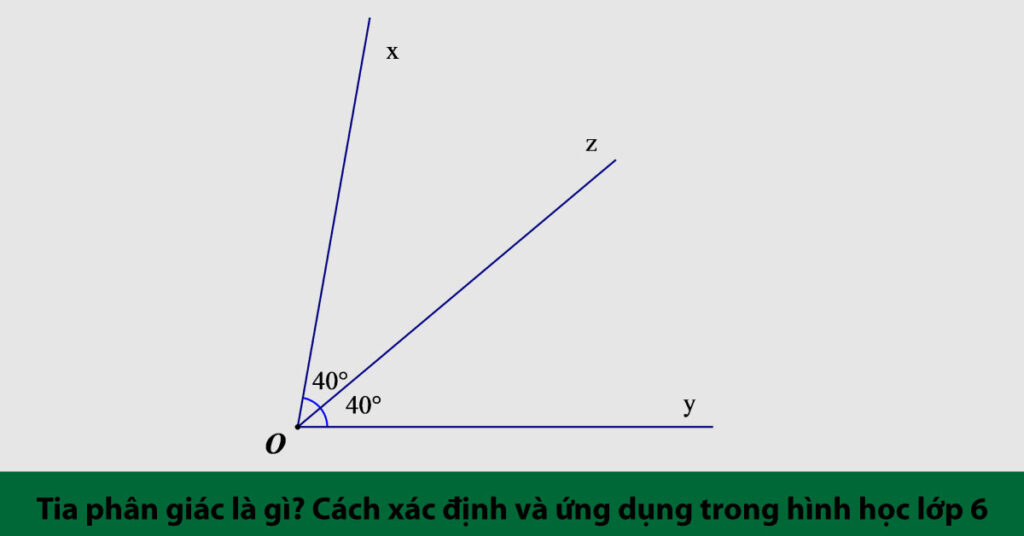
Vậy, câu trả lời cốt lõi cho tia phân giác là gì? Theo định nghĩa trong sách giáo khoa hình học, tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc nhỏ bằng nhau. Để một tia Oz là tia phân giác của góc xOy, nó phải thỏa mãn đồng thời hai điều kiện:
- Tia Oz phải nằm giữa hai tia Ox và Oy. Điều này có nghĩa là tia Oz phải xuất phát từ đỉnh O và nằm trong khoảng không gian của góc xOy.
- Tia Oz phải chia góc xOy thành hai góc có số đo bằng nhau. Tức là, góc xOz phải bằng góc zOy (∠xOz = ∠zOy).
Từ hai điều kiện này, chúng ta có thể suy ra rằng số đo của mỗi góc nhỏ. Nó sẽ bằng một nửa số đo của góc ban đầu: ∠xOz = ∠zOy = ∠xOy / 2. Mỗi một góc (không phải là góc bẹt) chỉ có duy nhất một tia phân giác. Khái niệm này rất đơn giản nhưng lại là nền tảng cho nhiều tính chất và định lý quan trọng.
2. Các Tính Chất Quan Trọng Của Tia Phân Giác – Tia Phân Giác Là Gì
Ngoài định nghĩa cơ bản, tia phân giác còn có một số tính chất hình học rất quan trọng. Những tính chất này thường được sử dụng để chứng minh các bài toán phức tạp hơn sau này.
- Tính chất 1 (Tính chất thuận):
- – Bất kỳ điểm nào nằm trên tia phân giác của một góc đều cách đều hai cạnh của góc đó.
- – Nghĩa là, nếu M là một điểm bất kỳ trên tia phân giác Oz của góc xOy. Và nếu ta kẻ các đường vuông góc từ M đến hai cạnh Ox và Oy (tại A và B). Thì độ dài của hai đoạn thẳng MA và MB sẽ bằng nhau (MA = MB).
- Tính chất 2 (Tính chất đảo):
- – Ngược lại, một điểm bất kỳ nằm bên trong một góc và cách đều hai cạnh của góc đó. Thì điểm đó phải nằm trên tia phân giác của góc đó.
- – Đây là tính chất đảo, giúp chứng minh một tia là tia phân giác.
Những tính chất này là cơ sở để giải thích tại sao ba đường phân giác trong một tam giác. Chúng lại đồng quy tại một điểm, điểm đó chính là tâm của đường tròn nội tiếp tam giác.
Hướng Dẫn Các Cách Vẽ Tia Phân Giác Chính Xác – Tia Phân Giác Là Gì
Có hai phương pháp chính để vẽ tia phân giác của một góc: dùng thước đo độ và dùng compa.
1. Cách 1: Vẽ Tia Phân Giác Bằng Thước Đo Góc (Thước Đo Độ)
Đây là cách vẽ dựa trên định nghĩa, rất trực quan và dễ thực hiện đối với học sinh.
- Các bước thực hiện:
- Bước 1: Đo góc ban đầu. Dùng thước đo độ để đo chính xác số đo của góc xOy cần vẽ tia phân giác. Giả sử bạn đo được góc xOy = 80°.
- Bước 2: Tính số đo góc cần chia. Lấy số đo của góc xOy chia cho 2. Trong ví dụ này, ta có: 80° / 2 = 40°.
- Bước 3: Vẽ tia phân giác. Vẫn giữ tâm thước tại đỉnh O và một cạnh (ví dụ Ox) trùng với vạch 0°. Tìm đến vạch 40° trên thước và đánh dấu một điểm (ví dụ điểm M).
- Bước 4: Nối và kết luận. Dùng thước thẳng, kẻ một tia có gốc tại O và đi qua điểm M vừa đánh dấu. Tia OM (hay Oz) chính là tia phân giác của góc xOy.
Cách này rất đơn giản nhưng độ chính xác phụ thuộc vào việc bạn đo góc và đánh dấu có chuẩn không.
2. Cách 2: Vẽ Tia Phân Giác Bằng Compa và Thước Kẻ (Cách Chuẩn Xác Nhất)
Phương pháp này không cần dùng đến thước đo độ nhưng lại cho kết quả chính xác tuyệt đối. Nó dựa trên tính chất “điểm nằm trên tia phân giác thì cách đều hai cạnh”.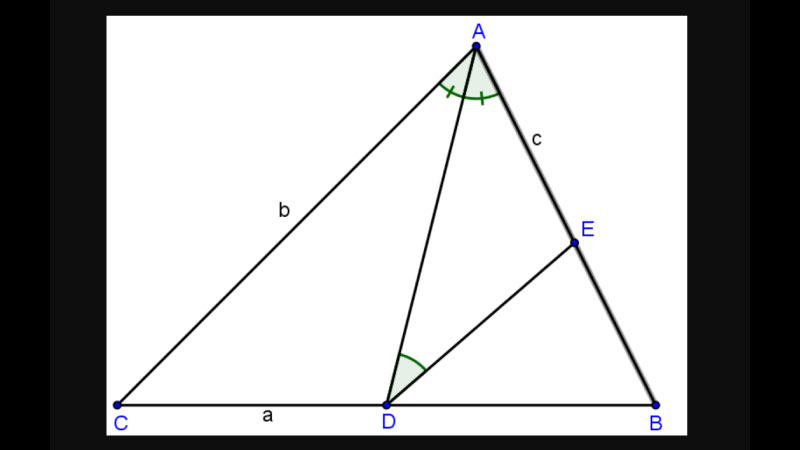
- Các bước thực hiện:
- Bước 1: Vẽ cung tròn thứ nhất. Đặt đầu nhọn của compa vào đỉnh O của góc xOy. Vẽ một cung tròn có bán kính bất kỳ, cắt hai cạnh Ox và Oy lần lượt tại hai điểm A và B.
- Bước 2: Vẽ hai cung tròn giao nhau. Giữ nguyên khẩu độ compa (hoặc thay đổi một khẩu độ mới lớn hơn một chút). Đặt đầu nhọn compa lần lượt vào hai điểm A và B vừa tạo. Vẽ hai cung tròn nhỏ sao cho chúng cắt nhau tại một điểm M nằm bên trong góc xOy.
- Bước 3: Vẽ tia phân giác. Dùng thước thẳng, kẻ một tia có gốc tại O và đi qua giao điểm M. Tia OM chính là tia phân giác cần vẽ.
Cách dựng hình này được sử dụng rất nhiều trong các bài toán chứng minh hình học. Nó thể hiện rõ bản chất và tính chất của tia phân giác một cách trực quan.
Tia Phân Giác Trong Tam Giác và Các Tính Chất Đặc Biệt – Tia Phân Giác Là Gì
Khái niệm tia phân giác có nhiều ứng dụng và tính chất quan trọng khi xét trong một tam giác.
1. Định Lý Về Ba Đường Phân Giác Trong Của Một Tam Giác – Tia phân giác là gì?
Trong một tam giác bất kỳ, mỗi góc đều có một tia phân giác của góc đó. Đoạn thẳng nối từ đỉnh đến cạnh đối diện của tia phân giác đó được gọi là đường phân giác. Một định lý rất quan trọng trong hình học phẳng phát biểu rằng: “Ba đường phân giác của một tam giác cùng đi qua một điểm (đồng quy)”. Điểm đồng quy này luôn nằm bên trong tam giác và có những tính chất rất đặc biệt. Nó là một trong bốn điểm đặc biệt của tam giác, bên cạnh trực tâm, trọng tâm và tâm đường tròn ngoại tiếp. Việc chứng minh định lý này dựa trên tính chất cơ bản của tia phân giác. Điểm giao của hai đường phân giác đầu tiên sẽ cách đều ba cạnh của tam giác. Do đó, nó cũng phải nằm trên đường phân giác thứ ba của tam giác đó.
2. Tâm Đường Tròn Nội Tiếp Tam Giác
Điểm đồng quy của ba đường phân giác trong của một tam giác được gọi là tâm của đường tròn nội tiếp tam giác. Đường tròn nội tiếp là đường tròn duy nhất nằm hoàn toàn bên trong tam giác. Và tiếp xúc với cả ba cạnh của tam giác đó một cách hoàn hảo. Lý do điểm đồng quy này là tâm đường tròn nội tiếp xuất phát từ tính chất của tia phân giác. Vì điểm này nằm trên cả ba đường phân giác, nó sẽ cách đều cả ba cạnh của tam giác. Khoảng cách từ điểm này đến mỗi cạnh chính là bán kính của đường tròn nội tiếp. Đây là một ứng dụng tuyệt vời, thể hiện mối liên hệ sâu sắc giữa các yếu tố trong hình học.
3. Định Lý Đường Phân Giác Trong Tam Giác (Angle Bisector Theorem)
Đây là một định lý quan trọng khác liên quan đến đường phân giác, thường được học ở các lớp cao hơn. Định lý này phát biểu rằng: “Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy”. Ví dụ, trong tam giác ABC, nếu AD là đường phân giác của góc A (D nằm trên BC). Thì ta sẽ có tỉ lệ thức: DB/DC = AB/AC. Định lý này rất hữu ích trong việc giải các bài toán liên quan đến tính toán độ dài. Hoặc chứng minh các tỉ lệ bằng nhau trong hình học tam giác phức tạp hơn. Nó cho thấy đường phân giác không chỉ chia đôi góc mà còn tạo ra một mối quan hệ tỉ lệ đặc biệt.
Kết Luận
Qua bài viết này, hy vọng các em học sinh và phụ huynh đã có câu trả lời chi tiết. Cho câu hỏi “tia phân giác là gì?” một cách đầy đủ và chính xác nhất. Đây là một khái niệm nền tảng nhưng cực kỳ quan trọng trong hình học phẳng. Việc hiểu rõ định nghĩa, nắm vững các tính chất và thành thạo các cách vẽ tia phân giác. Nó là chìa khóa để giải quyết tốt các bài tập liên quan và là cơ sở để học các kiến thức nâng cao.
Hãy thực hành vẽ tia phân giác bằng cả thước đo độ và compa để trở nên thành thạo. Đồng thời ghi nhớ các tính chất đặc biệt của nó trong tam giác, đặc biệt là tâm đường tròn nội tiếp. Việc nắm vững các khái niệm cơ bản ngay từ đầu sẽ giúp việc học hình học trở nên dễ dàng. Và thú vị hơn rất nhiều lần so với việc học thuộc lòng các công thức. Chúc các em có những giờ học hình học thật bổ ích và đạt được kết quả cao!